Проводится анализ некоторых аспектов принятия ответственным лицом управленческого решения, в частности, исследуются возможные ошибки и риски, возникающие из-за неправильности принятого решения, проводится анализ процедуры принятия решения, возникающие в связи с этим проблемы.
Ключевые слова: управленческое решение, принятие решения, информационные параметры, риски.
Рыночные отношения, в которых сегодня функционируют авиапредприятия, авиакомпании и различные компании, образующие инфраструктуру гражданской авиации, заставляют по новому подходить к такой классической проблеме, как управление этими структурами. Естественно, что принятие управленческих решений должно, прежде всего, опираться на имеющиеся исходные данные, которые в большинстве случаев могут носить только вероятностный характер, а коль скоро речь идет о рынке предоставляемых названными компаниями услуг, всегда необходимо учитывать определенную непредсказуемость происходящих событий, что требует введения в исходные данные вероятностных оценок. Таким образом, любое управленческое решение сопряжено с риском невыполнения поставленной задачи, измеряемой в виде вероятности такого события.
Для лица, принимающего решение (ЛПР), в основном необходимо знание двух аспектов: состояние рынка услуг, заданного через некоторые формальные характеристики, которые можно назвать информационными параметрами, и результаты деятельности компании на рынке, т.е. по своей сути формируемая компанией прибыль.
Итак JIПP, должно на основании названной информации, прежде всего, определить стратегию на рынке соответствующих услуг, в рамках которой принимать соответствующие управленческие решения.
На рис. 1 [1] показана общая схема принятия управленческих решений и их исполнения, а также источники ошибок и рисков, связанных с неоптимальными относительно выбранных критериев, решений. Из рисунка достаточно наглядно видно, где могут иметь место риски, т.е. потери, в конечном счете, в величине прибыли. Эти риски возникают вследствие:
- неоптимального (в рамках выбранного критерия при решении стратегической задачи компании) распределения имеющихся ресурсов между подпроцессами производства;
- неоптимального выбора (в рамках соответствующего критерия) управленческого критерия;
- неполноты имеющейся информации и ее частичной недостоверности;
- низкого уровня исполнения управленческих решений непосредственными исполнителями;
- недостаточной компетентностью лица, принимающего решения.
Нельзя не отметить, что рынок, и это исключительно принципиально, всегда функционирует в условиях статистической неопределенности, характеристики которого могут изменяться в достаточно широких пределах [1].
Таким образом, мы выходим на необходимость разработки моделей принятия управленческих решений, обеспечивающих повышение эффективности функционирования в условиях статистической неопределенности рынка, и оценок рисков, возникающих при этом.
Управление любой сложной системой неизбежно связано с выбором того или иного управленческого решения. В конечном счете, это решение должно способствовать реализации стоящей перед компанией целевой функции. Последнее слово в вопросе выбора решения принадлежит лицу, принимающему решение, выступающему в качестве абсолютно неизбежного атрибута любой сложной системы.
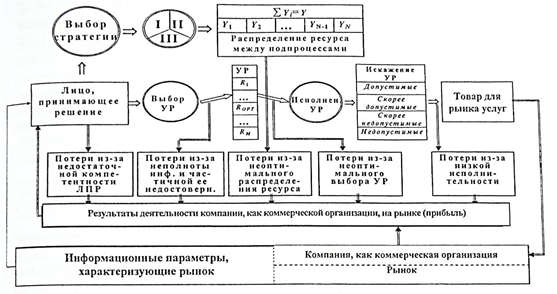
Рис. 1. Общая схема принятия управленческих решений и их исполнения, источники ошибок и рисков, связанных с неоптимальными относительно выбранных критериев, решениями.
ЛПР должно за заданное время обработать имеющуюся у него информацию и принять соответствующее решение.
В такой ситуации объективно приходится сталкиваться с рядом достаточно серьезных проблем.
Прежде всего, ЛПР должно суметь так обработать за время t, не больше заданного Т, т.е. (t ≤ Т) имеющуюся у него информацию, чтобы риски, т.е. принятое им управленческое решение наилучшим образом способствовало бы достижению решения стратегических или локальных тактических задач, стоящих перед компанией. Эту ситуацию можно формализовать следующим образом.
Во-первых, будем считать, что имеется некоторое информационное поле Q, содержащее разнообразную информацию, так или иначе влияющую на процесс принятия решения. Будем считать также, что это поле представляет собой совокупность из М информационных элементов
qi, где i = .
Во-вторых, аналогично можно считать, что имеется поле возможных решений - R, которые имеет право принять ЛПР. Вполне логично допустить, что это поле представляет собой совокупность из N возможных решений rj, где j =.
Наконец, должен существовать некоторый критерий оценки каждого из возможных решений rj, т.е. некоторый количественный показатель kj, характеризующий уровень достижения стоящей перед ЛПР стратегической или тактической задачи при принятии решения rj . Обратим внимание, что какое-то количество решений rj может не только не способствовать достижению поставленной цели, но даже приводить к обратному эффекту. В этой связи будем считать, что показатель kj может принимать как положительные, так и отрицательные значения.
Введение показателя kj дает возможность говорить о том, что одно из возможных решений лучше или хуже другого. Для определенности будем считать, что наилучшим решением будет некоторое решение rj0, которому соответствует максимальный показатель kj0. Для всех остальных решений этот показатель будет иметь меньшее значение.
В рамках проведенной достаточно естественной формализации можно ввести понятие идеального лица принимающего решения (ИЛПР), понимая под ним ЛПР, которое, располагая временем Т и всей необходимой для принятия решения информацией, примет именно решение rj0. Что касается неидеального ЛПР, то в этом случае можно говорить только о том, что решение rj0 может быть принято им с некоторой отличной от единицы вероятностью pj0, определяющей, в конце концов, именно риск этого решения.
Проведенная выше формализация, хотя и является достаточно логичной и последовательной, тем не менее, не учитывает объективно возникающие при принятии решения реалии и факторы.
Вновь вернемся к полю решений. Выбор решения rj0 напрямую связан с событиями и ситуациями во внешнем по отношению к организации мире, а поэтому не зависят от ЛПР. Следовательно, такой выбор не может быть проведен безошибочно, а поэтому, что исключительно принципиально, достоверно не могут быть определены ни показатель kj0, ни решение rj0. В этой связи естественно ввести вероятностные оценки показателя kj0 и говорить, что показателем эффективности решения rj0 является набор из S чисел kj0, где s =, с вероятностью появления числа, равной pjs0. В случае большого числа S целесообразнее перейти к непрерывной величине kj0, так что сказанное требует иного подхода к оценке риска, т.е. эффективности решения rj0, в качестве которого может быть принят переход к средним значениям и средним квадратичным отклонениям.
Одним из следствий сказанного является утверждение, что в случаях, когда соседние значения kj достаточно близки между собой, нецелесообразно различать между собой решения rj и rj+1. Это приводит к разумной необходимости объединять два или несколько соседних решений в один класс решений.
Рассмотренный подход относится к случаю статистически стабильных во времени внешних условиях (стационарные процессы), влияющих на значимость решений rj;. Ситуация, когда такой стабильности не наблюдается (нестационарные процессы), например, в форс-мажорных (в широком смысле понимания этого слова) условиях возможно потребуется использовать аппарат теории выбросов.
Перейдем к рассмотрению особенностей информационного поля. Как уже говорилось выше, информационное поле Q представляет собой совокупность из М информационных элементов qi, где i = .
В общем случае эти элементы можно разделить на две категории. В первую из этих категорий Q1 включим те из них, которые содержат информацию, необходимую для принятия решения. Во вторую Q2 – те, которые такой информации не несут.
Очень важный момент состоит в том, что среди информационных элементов, образующих Q1, имеются как элементы (их общее число обозначим М1), несущие достоверную информацию, так и элементы, несущие недостоверную информацию (их общее число обозначим М2 = М – М1). Совокупность первых элементов обозначим V1, а совокупность вторых – V2. Информационные элементы, входящие в совокупность V1, будем обозначать q1m, где m = , а в совокупность V2, как q2m, где m = . Здесь следует обратить внимание на два момента.
Даже в случае отсутствия недостоверной информации, когда V2 = Ø, может иметь место три ситуации. Первая из ситуаций предполагает, что имеющейся информации при ее правильной обработке вполне достаточно для принятия обоснованного решения rj0. Вторая ситуация имеет в виду, что в распоряжении ЛПР имеется излишняя информация даже по отношению к вопросу по обоснованию и принятию решения rj0. Обработка излишней информации, сверх той, которой вполне достаточно для обоснования решения rj0, требует излишнего отвлечения временного и материальных ресурсов. К третьей ситуации отнесем случай, когда имеющейся информации, содержащейся в совокупности V1, недостаточно для обоснования решения rj0. В этом случае ЛПР сможет обосновать иное, нежели rj0, решение rj. Сказанное выводит на определенный принцип ранжирования возможных решений. В этом случае решения следует располагать в порядке уменьшения используемого числа информационных элементов, необходимых для обоснования решения rj.
Наконец, необходимо обратить внимание на тот факт, что ЛПР принципиально считает, что вся информация, которую он извлекает из совокупности Q1, представляет собой достоверную информацию.
Рассматривая весь процесс выбора возможного решения в целом, следует учесть объективно возникающие факторы, влияющие на этот выбор.
Во-первых, ЛПР должно провести селекцию информационных элементов, отобрав из них только те, которые влияют на выбор решения. Обозначим вероятность правильного выбора как PC.
Во-вторых, ЛПР среди выбранных информационных элементов должен выделить те из них, которые несут достоверную информацию. Вероятность успеха этой операции обозначим PД.
В-третьих, ЛПР должен оценить внешнюю по отношению к его организации (структуре) среду с позиций ее влияния на целевую функцию организации. Вероятность правильной оценки этой операции обозначим PЦ.
В-четвертых, ЛПР, располагая отобранными им информационными элементами с учетом сделанной им оценки окружающей среды, должно выбрать одно из возможных решений rj. Вероятность правильного выбора обозначим PВ.
Таким образом, вероятность того, что ЛПР примет решение, адекватное реальной ситуации, наилучшим образом способствующим реализации целевой функции организации (структуры), будет равна: РУ = РСРДРЦРВ.
Наличие неизбежных ошибок при выборе решения приводит к тому, что выбор решения лицом, принимающим решение, представляет собой некоторое случайное событие, что дает возможность характеризовать его следующим образом.
Объективно, независимо от ЛПР, в каждой конкретной ситуации среди всего множества решений rj существует некоторое в рамках заданного критерия решение rj0, наилучшим образом способствующим достижению целевой функции организации (структуры). Обратим внимание, что в зависимости от объективного наличия тех или иных информационных элементов наилучшим может быть любое решение rj. Итак, пусть объективно для данной ситуации наилучшим в рамках сказанного является решение rj, где j= . ЛПР же, оценивая ситуацию с неизбежными ошибками, принимает решение rk, где k = , при этом оно считает, что принятое им решение является наилучшим. Обозначим вероятность этого события pjk. Таким образом, процесс выбора решения характеризуется набором из N2 вероятностей, которые удобно представить в виде некоторой матрицы Р, которую можно назвать матрицей рисков (перепутывания гипотез): Р = , i, k = .
Очевидно, что сумма элементов каждого столбца и каждой строки равны 1, т.е.
В матрице рисков на диагонали стоят вероятности того, что ЛПР выбрало в рамках используемого критерия наилучшее решение, соответствующее сложившейся ситуации. Все остальные элементы матрицы соответствуют вероятностям, когда выбранное решение не является оптимальным по выбранному критерию. Для ИЛIIP матрица рисков представляет собой единичную матрицу (диагональная матрица с единичными значениями на диагонали) размером NхN.
Следовательно, задача выбора управляющего решения по своей сути представляет собой задачу на проверку статистических гипотез (выбор решения rj) на основании имеющихся у него достоверных и недостоверных информационных элементов, т.е. в условиях частично достоверной информации.
Проиллюстрируем полученные результаты.
Рассмотрим задачу оптимизации выбора управленческого решения при нескольких различных критериях оптимизации на примере некоторой идеализированной модели рассматриваемой ситуации.
Будем считать, что каждый из информационных элементов принадлежит к одному из нескольких классов, объединяющих элементы, качество влияния которых на выбор решения (критерий Ω) примерно одинаково. Введем некоторую количественную меру Ki, характеризующую i-й информационный элемент. Его значение будет являться основанием для отнесения информационного элемента к тому или иному классу. В этом случае к m-му классу будем относить информационные элементы, у которых количественная мера Ki будет удовлетворять неравенству Kт-1 ≤ Kj < Kт.
Будем считать, что значимость каждого информационного элемента одинакова, а поэтому определяющую роль играет их количество.
Рассмотрим частный случай, когда число названных выше классов просто равно двум (это случай в общем не является таким уж частным, поскольку в большинстве случаев многие задачи подобного типа могут быть сведены к двухальтернативным задачам). Хотя такое допущение является известной идеализацией, тем не менее, на этом примере можно увидеть и оценить все аспекты рассматриваемой проблемы. В качестве обозначений введенных классов будем использовать буквы А и В. Будем считать, что, если все информационные элементы принадлежат классу А, то оптимальным решением будет r1. Если все информационные элементы принадлежат классу В, то оптимальным решением будет rN. В общем случае множество информационных элементов представляет совокупность элементов, принадлежащих как классу А, так и к классу В. При двухальтернативной ситуации необходимо введение некоторого граничного значения числа элементов, принадлежащих классу А, при котором еще необходимо принятие решения r1.
Пусть в класс А входит Т информационных элементов, тогда в класс В будет входить (М-Т) элементов. Будем считать, что, если Т T0 , объективно наилучшим решением будет решение r1. В противном случае, когда Т < T0 , должно быть принято решение r2.
В распоряжении ЛПР имеется М1<М.
Требуется по результатам анализа М1 информационного элемента дать заключение о выборе решения r1 или r2. С этой целью необходимо построить матрицу рисков для рассматриваемого случая.
Начнем с ситуации, когда объективно необходимо принять решение r1. Для полноты решения нужно знать априорную вероятность количества информационных параметров из их общего числа, удовлетворяющих условию Т T0.
Не составляет принципиального труда провести расчет элементов матрицы риска. Однако в виду громоздкости получающихся выражений в статье их явный вид не приводится.
Решающее правило, по которому ЛПР должно сделать выбор между r1 и r2, - единственно. Оно состоит в том, чтобы ввести пороговое значение тпор и при условии т тпор следует выбрать решение r1, а если m < mпор, то r2.
Для дальнейшего исследования целесообразно ввести понятие стоимости принятого решения Sij, где i, j = 1,2. В этом случае можно говорить об ожидаемой средней стоимости управленческих решений, которые соответствуют двум случаям: правильной и ошибочной оценкам ситуации. Средняя стоимость правильных решений будет: для 1-1 ситуации S11P11, а для 2-2 ситуации S22P22. Средняя стоимость ошибочных решений будет: для 1-2 ситуации S12P12, а для 2-1 ситуации S21P21.
Можно также говорить о средней стоимости принятия решения r1: = S11P11 + S21P21 и о средней стоимости принятия решения r1: = S12P12 + S22P22.
Полученные формулы открывают путь к построению ряда критериев, относящихся к тем или иным рискам. Среди них можно отметить следующие: первый – максимизация ; второй – максимизация ; третий - максимизация некоторой алгебраической суммы четвертый - минимизация стоимости ошибочных решений S21P21; пятый - минимизация стоимости ошибочных решений S12P12; шестой - минимизация алгебраической суммы ошибочных решений S21P21 + S12P12 и т.д. В качестве рабочего критерия оптимизации выбора управленческого решения можно брать любой из перечисленных критериев.
На практике большой интерес представляет решение задачи о минимизации риска, т.е. о минимизации стоимости ошибочных решений
Что касается определяющего элемента, от которого зависит искомая минимизация, то это - пороговый уровень тпор, а также небольшие вариации самого числа М1.
ЛИТЕРАТУРА
1. Елисеев Б.П. К вопросу оптимизации управленческих решений в вузе, выступающем в роли коммерческой организации // Научный Вестник МГТУ ГА. - 2010. - № 155.
